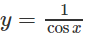Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:

a) f(x) = $\sqrt{(25-x^2)}$ trên đoạn [-4; 4]

b) f(x) = |$x^2$ – 3x + 2| trên đoạn [-10; 10]

c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]

d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]

Một chất điểm chuyển động theo quy luật s = 6$t^2$ – $t^3$. Tính thời điểm t (giây) tại đó vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất.

Giá trị lớn nhất của hàm số y = -$x^2$ + 4x - 5 trên đoạn [0;3] bằng:

A. -1              B. 1

C. 2              D. 0

Tìm hai số có hiệu là 13 sao cho tích của chúng là bé nhất

A. 13 và 0              B. 13/2 và -13/2

C. 15 và 2              D. 30 và 15

Giá trị nhỏ nhất của hàm số f(x) = $x^3$ + 3$x^2$ - 9x - 7 trên đoạn [-4;3] bằng:

A. -5              B. 0

C. 7              D. -12

Tìm các giá trị của m để phương trình : $x^3$ – 3$x^2$ – m = 0 có ba nghiệm phân biệt.

Hãy tìm tam giác vuông có diện tích lớn nhất nếu tổng của một cạnh góc vuông và cạnh huyền bằng hằng số a (a > 0).

Cho số dương m. Hãy phân tích m thành tổng của hai số dương sao cho tích của chúng là lớn nhất.

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau trên đoạn [2;4]

(Đề thi tốt nghiệp THPT năm 2008)

Giá trị lớn nhất của hàm số sau trên khoảng (-$\infty$; +$\infty$) là:

A. 1              B. 4/3

C. 5/3              D. 0

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau trên đoạn [0;2] bằng

A. 1/3 và -3              B. 3/2 và -1

C. 2 và -3              D. 1/2 và 5

Giá trị nhỏ nhất của hàm số sau trên khoảng (0; π/2) là:

A. 1              B. 2$\sqrt{2}$

C. -$\sqrt{2}$              D. 2/$\sqrt{2}$

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:

a) 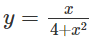 trên khoảng (−$\infty$;+$\infty$);

b)  trên khoảng